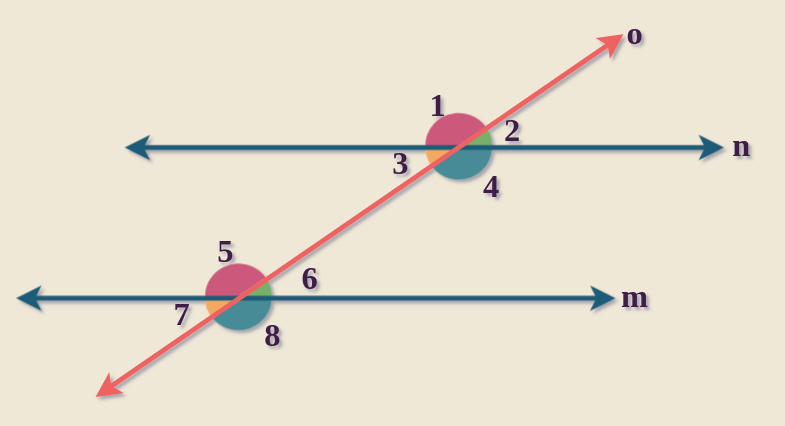
A transversal that crosses two lines forms an alternate interior angle. Alternate internal angles are those that develop inside the two lines and on opposing sides of the transversal. According to the theorem, the alternating internal angles are equal when the lines are parallel.
A transversal line intersecting two parallel lines results in alternate interior angles.
These are:
- On opposite sides of the transversal
- On the interior of the parallel lines
Key properties:
- Alternate interior angles are congruent (equal in measure)
- The sum of the two angles is 180 degrees
Here’s a diagram to visualize this:
For example, if one angle is 50°, the other must also be 50°. Their sum will always be 180°.
With the ability to determine missing angle measurements and demonstrate parallelism, these angle relationships help address geometry problems involving parallel lines and transversals.
If you have any further queries, please ask!
To give the angled color
Set the advanced tab’s dynamic color to Beta.
Red: (β ≤ 60°) * 1
Green: 155 / 255 * (β > 60°)
Blue: nil
green #009B00 if angle is more than 60°, otherwise red #FF0000